图的最短路径—BFS和Dijkstra算法

发表于 更新于 分类于 阅读次数： 本文字数： 3.6k 阅读时长 ≈ 7 分钟

BFS

使用场景

针对无权图，给定一个起始点，要求其他点到起始点的最短路径，可以使用BFS（广度优先搜索）算法得出结果。

代码实现和原理分析

给出下面一个图，假设起始点为3

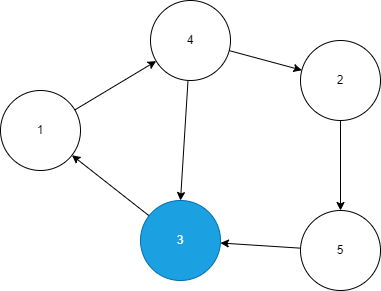
有向无权图

使用distance数组和visited数组分别记录每个点的最短路径和该点是否被访问过。

如需记录最短路径，则需要path数组

1
2
3
vector<int> distance(n+1, -1); // -1表示距离无穷大 如果遍历结束后distance[i]为-1 则表示与这个节点不相通
vector<bool> visited(n+1, false); // 初始化为false 表示默认都没访问到
vector<int> path(n+1, -1); // 记录前驱节点

对于起始点，其distance[start]应该初始化为0， visited[start]初始化为true

1
2
distance[start] = 0;
visited[start] = true;

开始广度优先搜索，依次标记每个未访问的节点为访问状态，这样做可以保证最短路径的节点，最先被标记， 同时也可以避免成环问题 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
queue<int> q;
q.push(start);

while (!q.empty()) {
    int size = q.size();
    while (size--) {
        int cur = q.front();
        q.pop();
        // 遍历邻居
        for (auto neighbor : graph[cur]) {
            if (!visited[neighbor]) {
                distance[neighbor] = distance[cur] + 1;
                path[neighbor] = cur;
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }
}

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int main() {
	// 构造图
	vector<vector<int>> graph{ {}, {4}, {5}, {1}, {3, 2}, {3} };
	int n = 5;
	vector<int> distance(n + 1, -1);
	vector<int> path(n + 1, -1);
	vector<bool> visited(n + 1, false);
	distance[3] = 0;
	visited[3] = true;

	// 开始广度优先搜索
	queue<int> q;
	q.push(3);
	while (!q.empty()) {
		int size = q.size();
		while (size--) {
			int cur = q.front();
			q.pop();
			for (auto neighbor : graph[cur]) {
				if (!visited[neighbor]) {
					distance[neighbor] = distance[cur] + 1;
					path[neighbor] = cur;
					visited[neighbor] = true;
					q.push(neighbor);
				}
			}
		}
	}

	// 打印distance数组
	for (auto i : distance) {
		cout << i << ' ';
	}
	// 打印path数组
	cout << endl;
	for (auto i : path) {
		cout << i << ' ';
	}

	return 0;
}

时空复杂度分析

因为需要访问所有节点（最坏情况下）所以时间复杂度应该为 O(V+E) n为节点数量

空间复杂度 考虑到distance、visited和path数组的开销 应为O(V)

Dijkstra算法

使用场景

针对有权图，求最短路径问题，这里介绍的是使用堆进行优化的Dijkstra算法，而非暴力的Dijkstra算法

代码实现和原理分析

给出一个有权图，起点为1

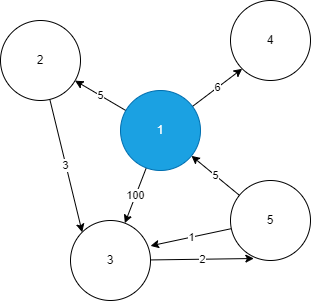
有向有权图

Dijkstra算法的具体步骤，可以分为以下几点：

  1. 创建distance数组和visited数组，分别用于记录最短路径和该节点是否已被访问，这里的visited，还有另一层含义，即表示该节点的最短路径是否已经确定。
  2. 初始化distance和visited数组，设置distance[start] = 0;，同时需注意distance数组中的初始值要尽可能大
  3. 建立小根堆，将初始节点压入堆中
  4. 从小根堆中弹出元素
    1. 如果该节点未访问过 则visited[cur] = true;
    2. 如果该节点已访问过 则continue
    3. 处理各边
      1. 如果!visited[neighbor] && distance[cur] + weight < distance[neighbor]，则进行更新，即distance[neighbor] = distance[cur] + weight; q.push(neighbor);
      2. 其他情况不处理
    4. 重复第4步骤，直到小根堆为空

具体的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

// Dijkstra
// 创建图
vector<vector<vector<int>>> graph{ {{}}, {{2, 5}, {3, 100}, {4, 5}}, {{3, 3}}, {{5, 2}}, {{}}, {{1, 5}, {3, 1}} };
int start = 1, n = 5;

vector<int> distance(n + 1, INT_MAX);
vector<bool> visited(n + 1, false);
distance[start] = 0;

auto cmp = [](vector<int>& a, vector<int>& b) -> bool {
	return a[1] > b[1];
	};
// 使用优先队列创建小根堆
priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)>q(cmp);
q.push({ start, 0 });

while (!q.empty()) {
	vector<int> cur = q.top();
	q.pop();
	if (visited[cur[0]]) continue;
	visited[cur[0]] = true;
	// 处理各边
	for (auto neighbor : graph[cur[0]]) {
        // neighbor.size() > 0判空
		if (neighbor.size() > 0 && !visited[neighbor[0]] && cur[1] + neighbor[1] < distance[neighbor[0]]) {
			distance[neighbor[0]] = cur[1] + neighbor[1];
			q.push({neighbor[0], distance[neighbor[0]]});
		}
	}
}

// 打印distance数组
for (auto i : distance) {
	cout << i << ' ';
}

时空复杂度分析

因为要遍历每一条边和每一个节点且要经过堆的调整 所以时间复杂度为 O((V + E) log V)
空间复杂度显然为 O(V)