平衡二叉树(AVL树)与二叉搜索树

发表于 更新于 分类于 阅读次数： 本文字数： 4.1k 阅读时长 ≈ 7 分钟

二叉搜索树/二叉排序树定义

满足以下特征的二叉树，即为二叉搜索树：

  1. 若左子树非空，则左子树上的所有节点要小于根节点
  2. 若右子树非空，则右子树上的所有节点要大于根节点
  3. 所有子结构满足上面两个条件

平衡二叉树的定义

平衡二叉树，满足以下特征：

  1. 左右子树的高度差不超过1
  2. 所有子结构满足条件1

使用平衡二叉树优化二叉搜索树

二叉搜索树在理想情况下查找效率是O(logn)的，但是在最坏情况下是O(n)的，比如下面这种情况:

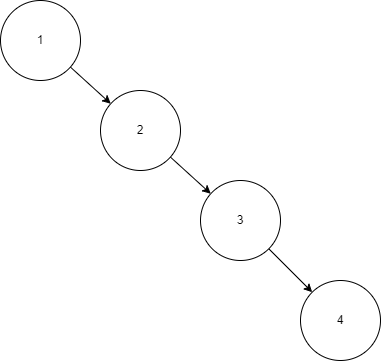
二叉搜索树

但如果将这个二叉搜索树变为平衡二叉树，效率会得到大大提高，如下图：

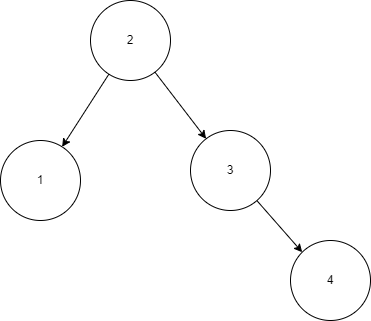
优化后的二叉搜索树

左旋和右旋

左旋和右旋是调整二叉树为平衡二叉树的两大“武器”

左旋

  • 适用范围

当最小失衡二叉树出现以下情况时，可以使用左旋进行调整

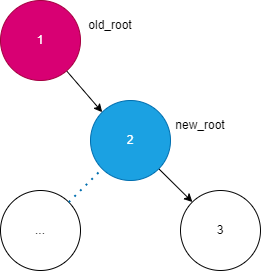
可以左旋的情况

基本的步骤是：

  1. 将old_root的右孩子new_root作为新的根节点
  2. 如果new_root有左孩子，则将这个左孩子当做old_root的右孩子
  3. 将new_root的做左孩子设为old_root
  • 模版代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

// 左旋
Node* leftRotate(Node* root) {
	Node* newRoot = root->right;
	Node* tmp = newRoot->left;

	root->right = tmp;
	newRoot->left = root;

	// 更新高度
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));
	newRoot->height = 1 + max(getHeight(root), getHeight(newRoot->right));
	return newRoot;
}

右旋

  • 适用范围

当最小失衡二叉树出现以下情况时，可以使用右旋进行调整

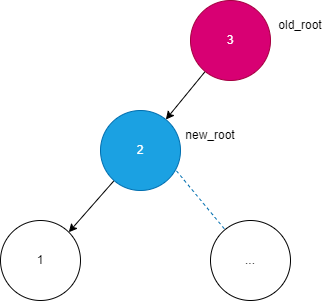
可以右旋的情况

基本的步骤是：

  1. 将old_root的左孩子new_root作为新的根节点
  2. 如果new_root有右孩子，则将这个右孩子当做old_root的左孩子
  3. 将new_root的右孩子设为old_root
  • 模版代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

// 右旋
Node* rightRotate(Node* root) {
	Node* newRoot = root->left;
	Node* tmp = newRoot->right;

	root->left = tmp;
	newRoot->right = root;

	// 更新高度
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));
	newRoot->height = 1 + max(getHeight(newRoot->left), getHeight(root));
	return newRoot;
}

四种类型

LL

LL类型情况如下：

LL类型

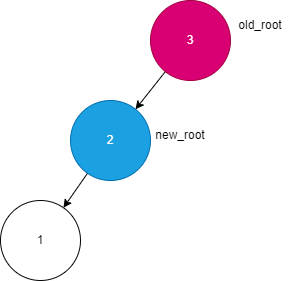
判断条件：

  1. old_root的平衡因子大于1
  2. new_root的平衡因子大于0

只需对old_root进行右旋即可

1
2
3

if (getBalance(root) > 1 && getBalance(root->left) > 0) return leftRotate(root);

LR

LR类型情况如下:

LR类型

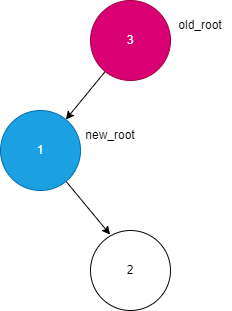
判断条件：

  1. old_root的平衡因子大于1
  2. new_root的平衡因子小于0

操作步骤：

  1. 先对new_root进行左旋
  2. 再对old_root进行右旋
1
2
3
4
if (getBalance(root) > 1 && getBalance(root->left) < 0) {
	root->left = leftRotate(root->right);
	return rightRotate(root);
}

RR

RR类型情况如下：

RR类型

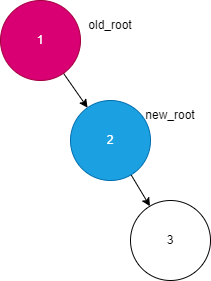
判断条件：

  1. old_root的平衡因子小于-1
  2. new_root的平衡因子小于0

只需对old_root进行左旋即可

1
2
3

if (getBalance(root) < -1 && getBalance(root->right) < 0) return rightRotate(root);

RL

RL类型情况如下：

RL类型

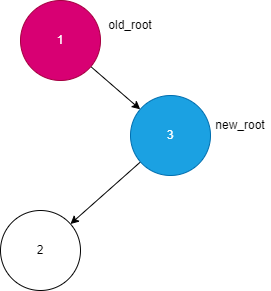
判断条件：

  1. old_root的平衡因子小于-1
  2. new_root的平衡因子大于0

操作步骤：

  1. 先对new_root进行右旋
  2. 再对old_root进行左旋
1
2
3
4
5
6

if (getBalance(root) < -1 && getBalance(root->left) > 0) {
	root->right = rightRotate(root->right);
	return leftRotate(root);
}

插入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

// 插入节点
Node* insert(Node* root, int val) {
	if (!root) return new Node(val);
	if (val > root->val) {
		root->right = insert(root->right, val);
	}
	else if (val < root->val) {
		root->left = insert(root->left, val);
	}
	else {
		return root;
	}

	// 更新高度
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));

	// 平衡性调整
	if (getBalance(root) < -1) {
		// RL
		if (getBalance(root->right) > 0) {
			root->right = rightRotate(root->right);
			return leftRotate(root);
		}
		// RR
		else {
			return leftRotate(root);
		}
	}
	else if (getBalance(root) > 1) {
		// LR
		if (getBalance(root->left) < 0) {
			root->left = leftRotate(root->left);
			return rightRotate(root);
		}
		// LL
		else {
			return rightRotate(root);
		}
	}
	return root;
}

删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

// 删除节点
Node* delete_node(Node* root, int val) {
	if (!root) return root;
	if (root->val == val) {
		if (!root->left && !root->right) {
			return nullptr;
		}
		else if (root->left && !root->right) {
			return root->left;
		}
		else if (!root->left && root->right) {
			return root->right;
		}
		else {
			Node* tmp = root->right;
			while (tmp->left) tmp = tmp->left;
			tmp->left = root->left;
			return root->right;
		}
	}
	if (val > root->val) root->right = delete_node(root->right, val);
	if (val < root->val) root->left = delete_node(root->left, val);

	if (!root) return nullptr;

	// 更新树高
	root->height = 1 + max(getHeight(root->left), getHeight(root->right));

	// 调整二叉树
	// LL
	if (getBalance(root) > 1 && getBalance(root->left) >= 0) {
		return rightRotate(root);
	}
	// LR
	if (getBalance(root) > 1 && getBalance(root->left) < 0) {
		root->left = leftRotate(root->left);
		return rightRotate(root);
	}
	// RR
	if (getBalance(root) < -1 && getBalance(root->right) <= 0) {
		return leftRotate(root);
	}
	// RL
	if (getBalance(root) < -1 && getBalance(root->right) > 0) {
		root->right = rightRotate(root->right);
		return leftRotate(root);
	}
	return root;
}